Mastering Mental Ability: Inequality
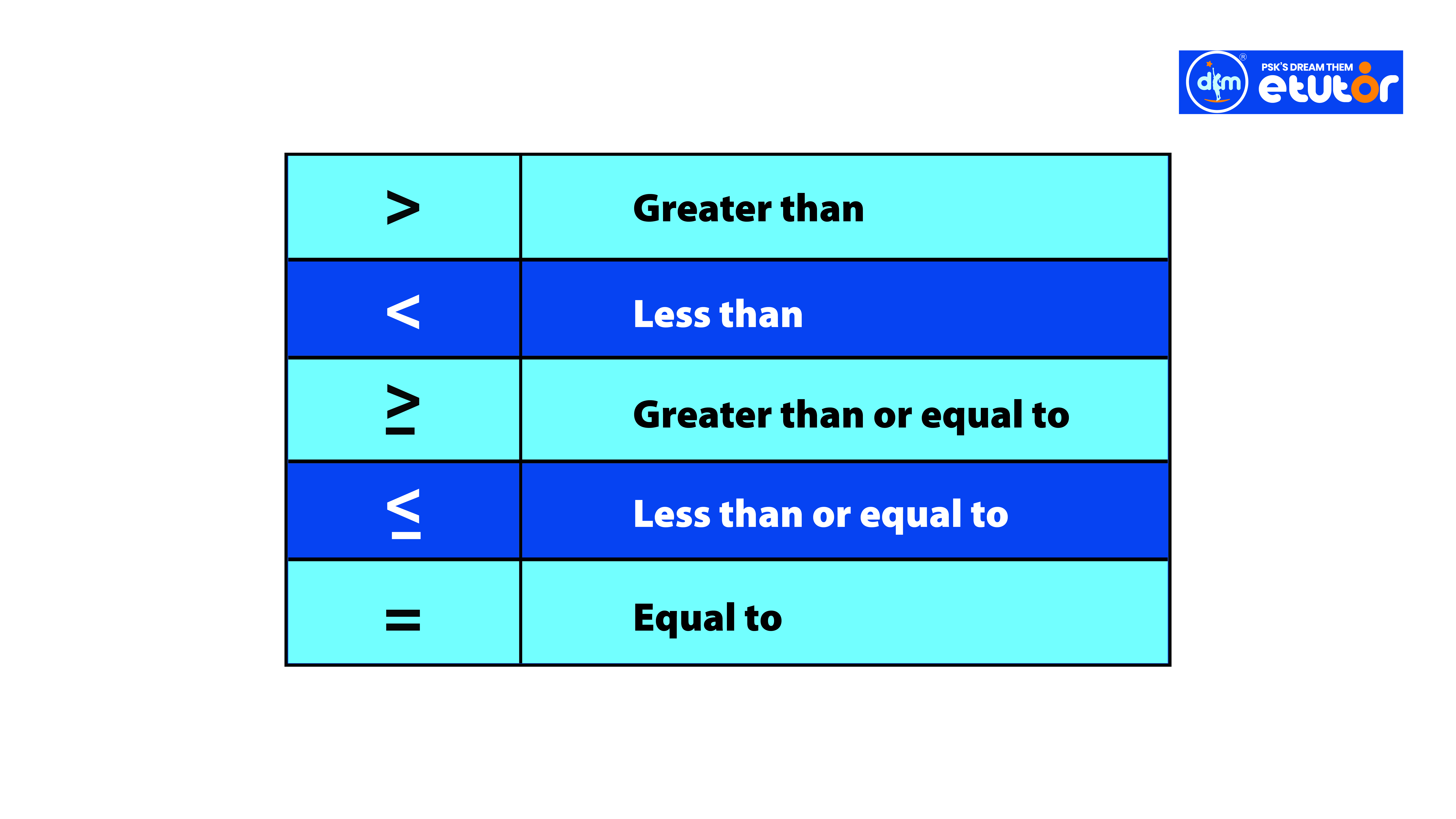
Inequality is one of the very important topics in all competitive examinations and scholarship examinations. It is all about dealing with these set of symbols, greater than, lesser than, greater than or equal to, less than or equal to, and equal to.
Two real numbers or two algebraic expressions related by the symbols <, >, = or = form an inequality.
Equal numbers may be added to (or subtracted from) both sides of an inequality. Both sides of an inequality can be multiplied (or divided) by the same positive number. But when both sides are multiplied (or divided) by a negative number, then the inequality is reversed.
The values of x, which make an inequality a true statement, are called solutions of the inequality.
Questions And Answers
1. Example 1:
Answer: The solution is 2x + 3 < 9
- 1. Start with the inequality: 2x + 3 < 9.
- 2. To isolate x, subtract 3 from both sides: 2x + 3 - 3 < 9 - 3.
- 3. Simplify to get: 2x < 6.
- 4. Next, divide both sides by 2 to solve for x: x < \frac{6}{2}.
Simplify to get: x < 3.
2. Example 2:
Question: Solve 5y - 2 > 13
Solution:
- 1. Start with the inequality: 5y - 2 > 13.
- 2. To isolate y, add 2 to both sides: 5y - 2 + 2 > 13 + 2.
- 3. Simplify to get: 5y > 15.
- 4. Next, divide both sides by 5 to solve for y: y > 15 / 5.
Simplify to get: y > 3.
Answer: The solution is y > 3.
3. Example 3:
Question: Solve X < M > L > Z
Solution:
- 1. Start with the given inequalities: X < M, M > L, L > Z.
- 2. Conclusion 1: X > Z
- Let's analyze Conclusion 1: X > Z
- From L > Z, we have Z < L.
- From M > L, we have M > L > Z.
- From X < M, we have X < M.
- Combining these inequalities, we get X < M > L > Z.
- This sequence implies X > Z because X < M and Z < L, so X > Z.
- Therefore, Conclusion 1 X > Z is true.
- 3. Conclusion 2: Z < M
- Let's analyze Conclusion 2: Z < M
- From the given inequalities: M > L > Z
- Since M > L and L > Z, it follows that M > Z.
- Therefore, Conclusion 2: Z < M is true.
Conclusion Summary:
- Conclusion 1: X > Z is true.
- Conclusion 2: Z < M is true.
Thus, the solutions to the conclusions are:
- Conclusion 1: True
- Conclusion 2: True
