Mastering Mental Ability:Venn Diagrams
Venn Diagram is a type of a diagram used to show the logical relation between sets. Venn diagrams are often called set diagrams or Logic diagrams as they show the relation between sets. These are widely used in Mathematics, Statistics, Linguistics, Logic, Teaching, Computer Science and Business. Venn diagrams consist of multiple overlapping circles. Each represent a set. The areas where the circles overlap shows elements that are common to both sets. Venn diagram was introduced by the English logician John Venn. He popularized this concept in the 1880's. The main use of Venn diagram is that it allows users to visualise the information. It shows the similarities and difference between concepts.
Venn Diagram of Three Sets
Check the Venn diagram of three sets given below.

Total = |A| + |B| + |C| - |AnB| - |AnC| - |BnC| + |AnBnC|
Venn Diagram Symbols
The symbols commonly used to represent set operations in Venn diagrams are:
- Union of sets: ∪
- Intersection of sets: ∩
- Complement of a set: A' or Aⁿ
Operations on Venn Diagrams
1. Union of Sets
The union of sets combines all elements from two or more sets.
2. Intersection of Sets
The intersection of sets includes only elements that are common to all sets.
3. Difference of Sets
The difference of sets includes elements that are in one set but not in another.
4. Complement of Sets
The complement of a set includes all elements in the universal set that are not in the specified set.
Union of Two Sets
The union of two sets A and B, denoted by A ∪ B, is the set containing all elements that are in A, in B, or in both.
Symbolically: A ∪ B = {x | x ∈ A or x ∈ B}
.jpg)
Union of Two Sets
Example: Union of Sets A and B
Let A = {1,2,3,4,5} and B = {6,7,8,9,10}.
The union A?B is :
AUB = {1,2,3,4,5,6,7,8,9,10}
Properties of Union and Related Symbols
| Property | Description |
|---|---|
| Associative Property: | ( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) |
| Idempotent Property: | A ∪ A = A |
| Identity Law (Property of Empty Set): | A ∪ ∅ = A |
| Property of Universal Set: | A ∪ U = U |
| Intersection Symbol: | A ∩ B |
| Complement Symbol: | A' or A ⁿ |
The Intersection of Sets
The intersection of two sets A and B, denoted by AnB, is the set containing all elements that are both in A and in B.
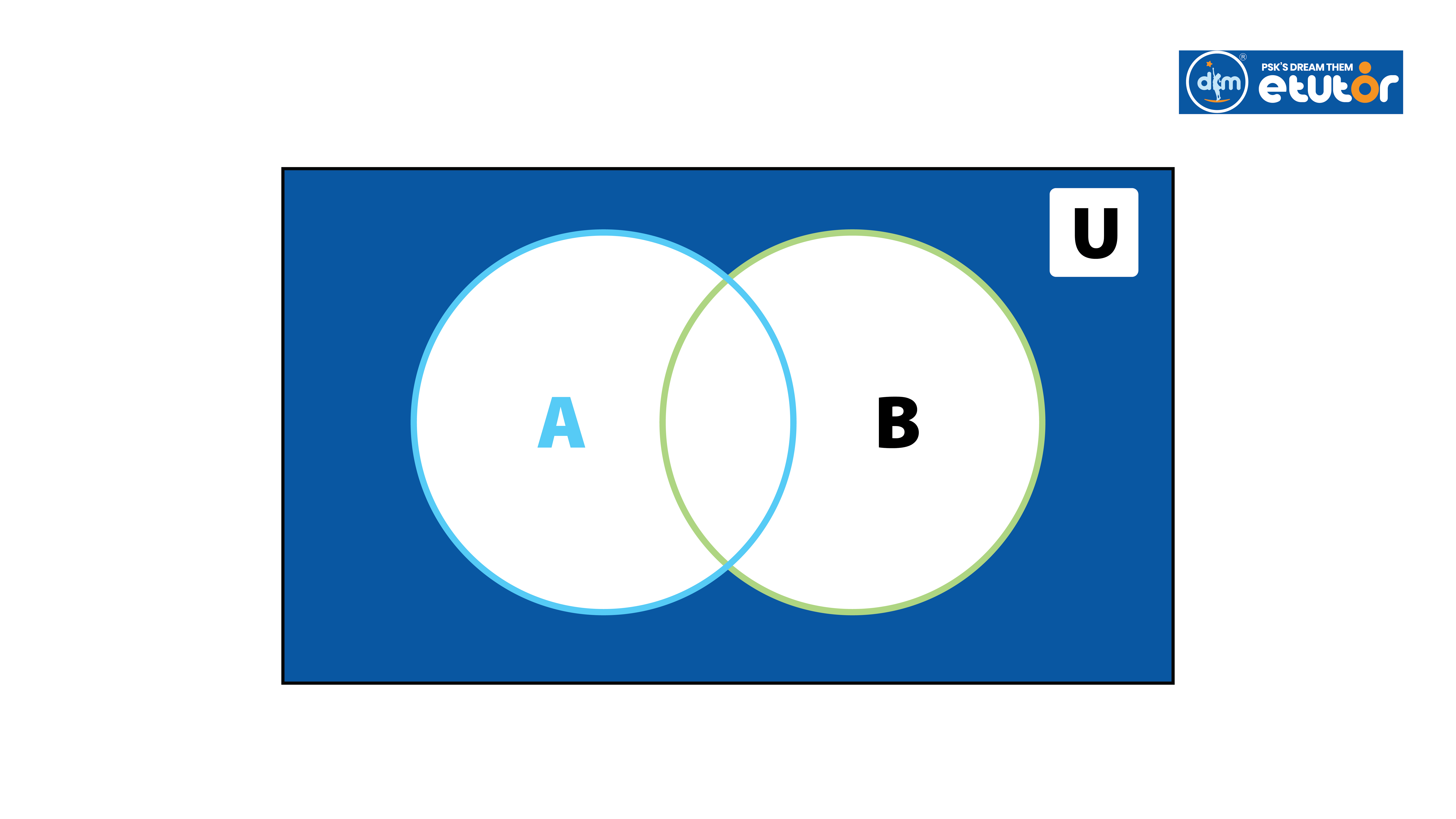
Union of Two Sets
Properties of Intersection of Sets
| Property | Description |
|---|---|
| Commutative Law: | A ∩ B = B ∩ A |
| Associative Law: | (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Law of Empty Set: | ∅ ∩ A = ∅ |
| Law of Universal Set: | U ∩ A = A |
| Idempotent Law: | A ∩ A = A |
Examples
Let A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8, 10}
The intersection A ∩ B is:
A ∩ B = {2, 4}
Difference of Sets
The difference of two sets A and B, denoted by A-B or A\B, is the set of elements that are in A but not in B.
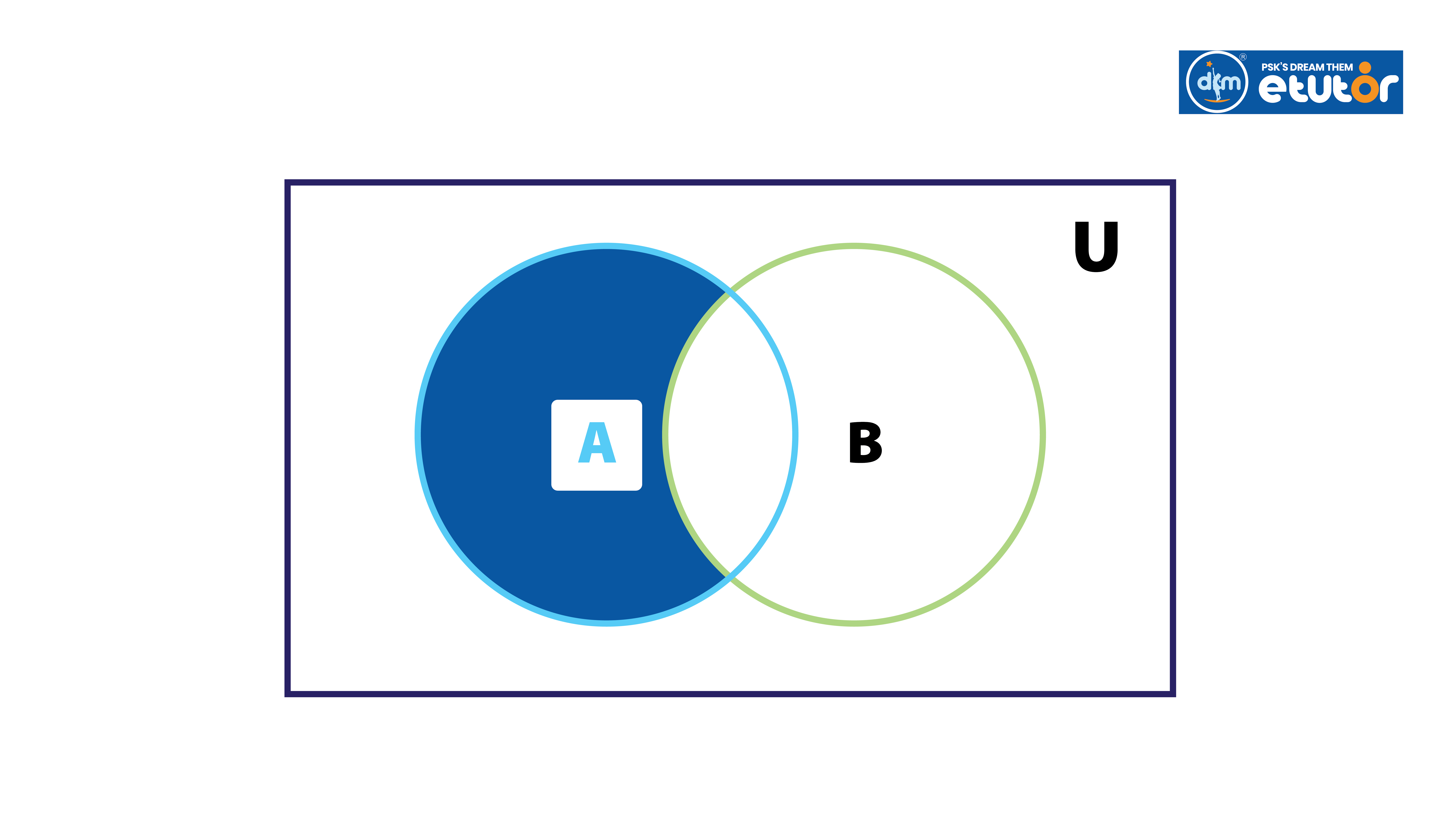
Difference between Two Sets
Examples:
Let A = {1, 2, 3, 4, 5} and B = {3, 4, 5}
A - B = {1, 2}
Symmetric Difference between Two Sets
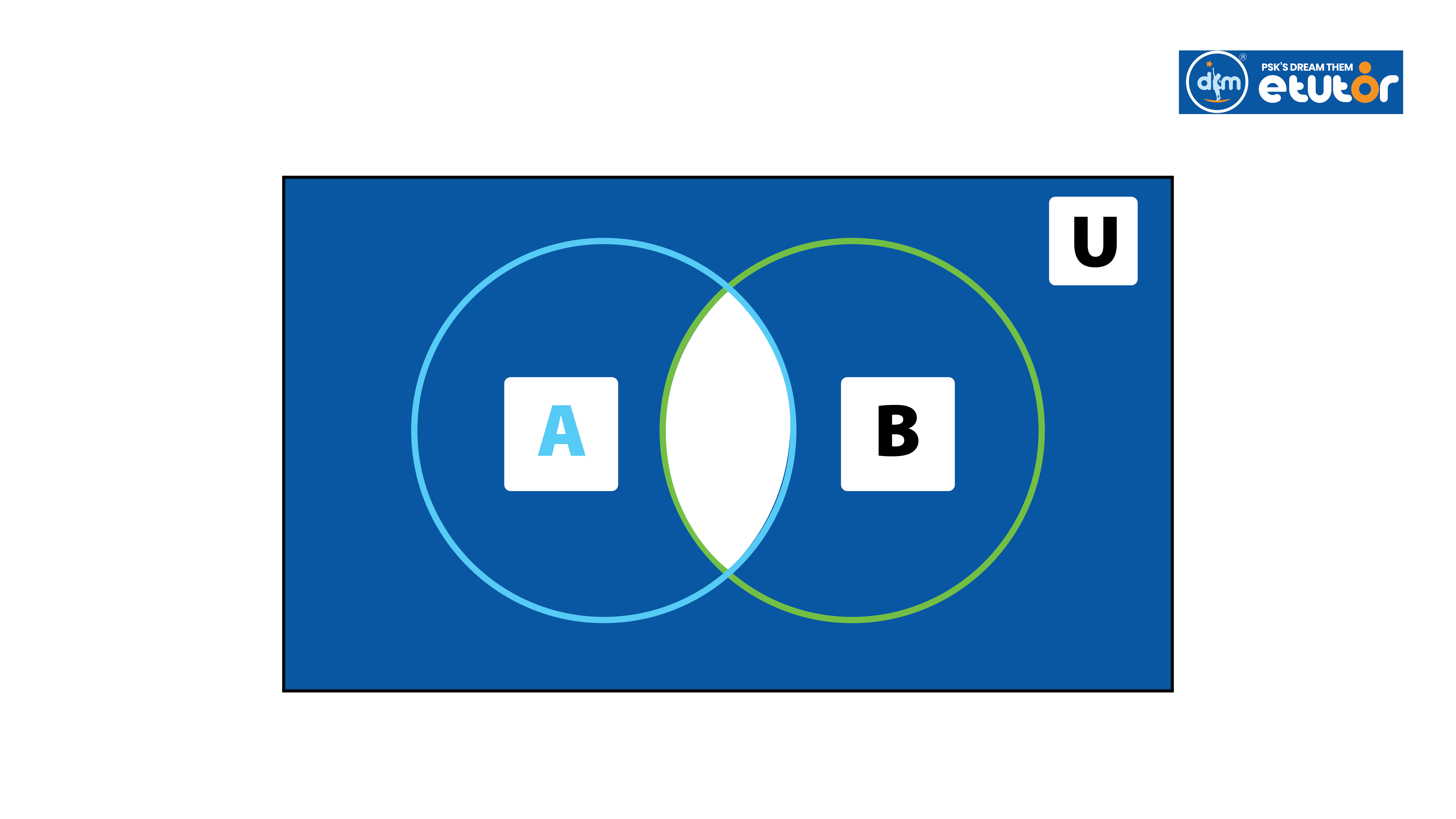
Difference between Two Sets
Complement of a Set
The complement of a set A, denoted by A', is the set of all items in the universal set U that are not in A.
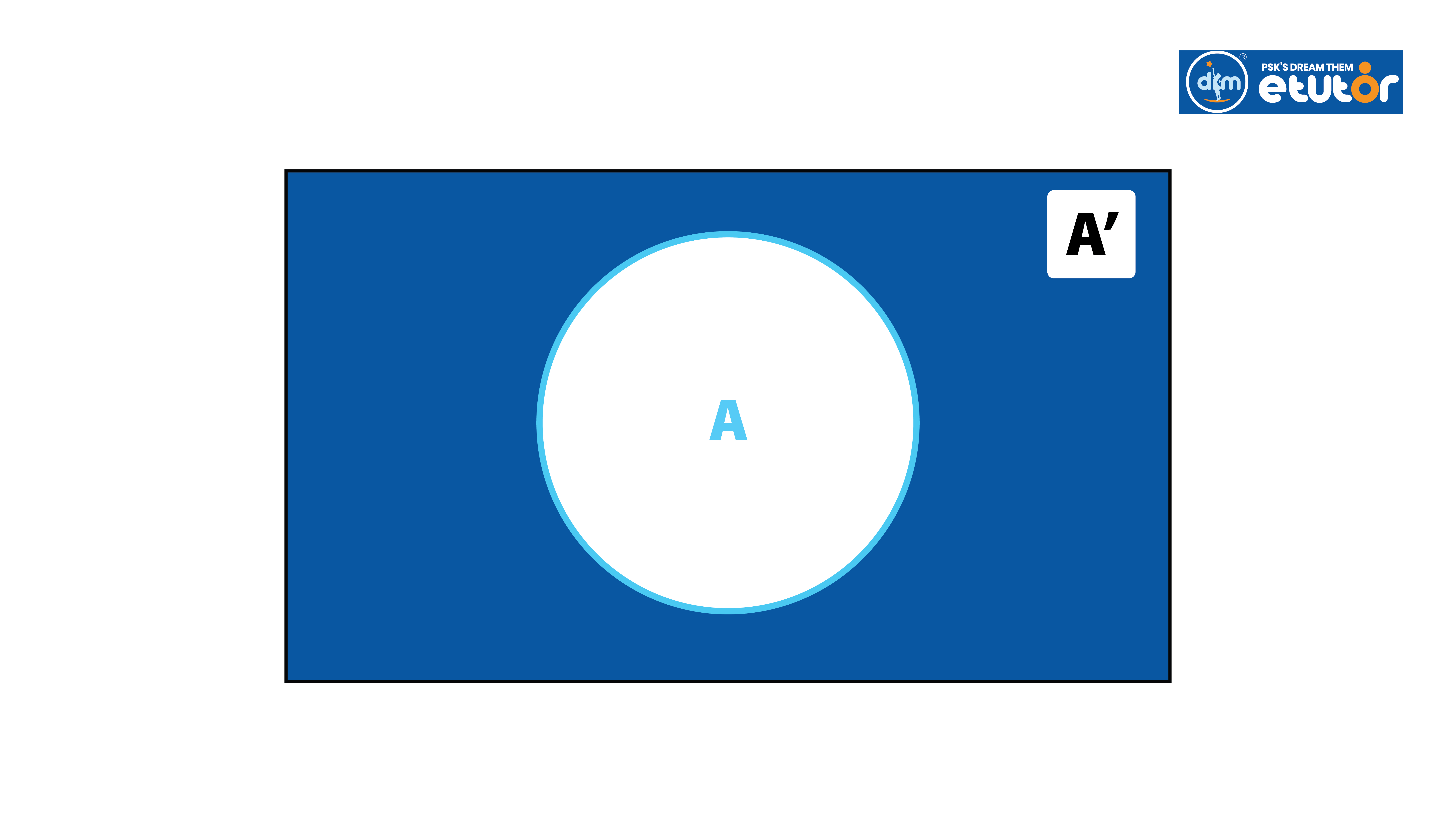
Additional Properties:
A + A' = U
It means that the set formed with elements of set A and set A' combined is equal to U.
(A')' = A
This property states that the complement of the complement of set A is equal to A itself.
Example:
Let U = {1, 2, 3, 4, 5, 6} and A = {1, 3, 5}
A' = {2, 4, 6}
